Behavioural Genetic Interactive Modules

Correlation & Regression



Overview

This module aims to introduce the related concepts of correlation and regression and to demonstrate their relationship with variance and covariance.

Tutorial

As mentioned in the previous module, in order to assess the magnitude of a covariance statistic we can use information about the variances of the measures to standardise it. We can also calculate so-called regression coefficients easily from the covariance if we know the variance of the measures.

This module allows the user to explore these related measures by simulating a bivariate dataset with certain known properties.

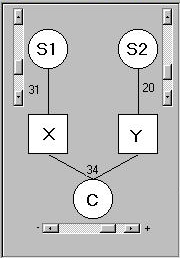This panel is used to specify the relationship between the two simulated variables, X and Y. It represents three separate influences, or sources of variation, on the two measures:

  • S1 is some unmeasured, or latent, variable that directly influences X only
  • S2 is some unmeasured variable that directly influences Y only
  • C influences both X and Y (although, as we shall see, it can influence X and Y similarly, or it can influence them differentially
Imagine the following scenario to make this more concrete: imagine two boys, Mike and Joe, who both attend the same school. If we were to look at all results they obtained in all the tests they performed at school, we could ask whether or not their scores tended to be related.

By related in this context, we do not just mean similar. For example, Mike could consistently score 20 points below Joe, and so they would have quite dissimilar mean scores. What we mean here by related is that on the tests where Mike tends to score higher than he usually does, so does Joe. In statistical language, we ask whether these measures are correlated.

In this scenario,
  • X represents Mike's test scores
  • Y represents Joe's test scores
  • S1 represents all of the influences specific to Mike that impact upon his test scores: for instance, whether or not his mother helps him with his homework, Mike's own IQ, etc.
  • S2 represents the factors that are specific to Joe
  • C represents the factors that influence their test scores that are shared by both Mike and Joe: for instance, the teachers they share for different subjects. If some teachers are better than others, and this influences their scores similarly, this shared factor will tend to induce a correlation between Mike's and Joe's scores.
The sliders determine how much of an influence these different sources of variance have on X and Y. The scales are arbitrarily set between 0 to 100 for the two specific measures and -50 to 50 for the shared measure. A negative value for the shared source of variance does not mean that the mean score of both Mike and Joe would go down (remember: this entire module is not concerned with mean differences). Rather, a negative value here means precisely the opposite of sharing - this factor tends to make Mike and Joe less similar. Be careful with the language here - although S1 and S2 are not 'shared' with each other, they neither make the two boys' scores similar nor dissimilar to each other. They are said to be independent from one another.

Moving the sliders causes the module to begin simulating normally-distributed data. The number of datapoints is determined by the slider in the sample size panel, which can be between 5 and 500. (Perhaps we should stop the analogy with Mike and Joe here - it would be rather unfair to make them do 500 tests!)

Note that if you set all the sliders to zero (which would imply no variation for either measure) the module will 'compensate' by introducing a small amount of shared variation. If it did not do this, an error would occur when calculating the bivariate statistics (it would imply division by zero). In any case, the concept of covariation is meaningless if there is no variation in at least one of the measures.

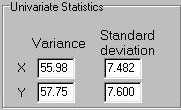This module does not show us the individual data points, unlike the previous two modules (although we will see a scatter-plot of all the points). Instead, just the summary statistics are presented, now that we know how they are calculated. The univariate statistics presented are the variance and the standard deviation for X and Y.

Note the effect of moving the sliders on these variance estimates. Firstly, note they that will tend to 'jump around' quite a lot. This is because of random sampling variation. When we specify the strengths of S1, S2 and C in the panel above, we are specifying the population parameters. The computer then acts as if it were randomly selected between 5 and 500 (however many as specified) individuals from this population. So, on average, we should expect the sample to be representative of the population.

But we also expect sample-to-sample variation in these estimates. We should also expect that this sample-to-sample variation is greater if the samples drawn are of a relatively small size. Confirm this for yourself by making the sample size smaller. The sliders at the top directly represent the variance in X and Y attributable to the three causal factors. The estimated sample variance for X and Y should therefore be close to the sum of these values (i.e. S1+C for X and S2+C for Y): this will be more likely to be the case when the sampe size is larger. Note that it is the absolute value of C that contributes to the variance, however. That is, if S1 were 50 but C were -25, we should expect the variance of X to be 75 and not 25. This is because C still generates variation in X - if we are not considering the relationship between X and Y, then the sign of C is meaningless.

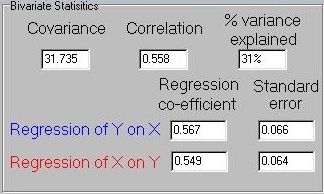The sign of C will not be meaningless when considering the bivariate statistics, however. These statistics are essentially trying to quantify the extent of the relationship between X and Y. In this context, they are evaluating the magnitude and sign of the shared cause, C, relative to the magnitudes of the specific causes, S1 and S2. The presentation in terms of the shared and nonshared latent variables is arbitrary, however. See the Appendix for a discussion of the possible reasons for observing associations between two variables: having a shared cause is only one of them.

First, we see that the covariance between X and Y has been calculated. Inside the module, this would have followed exactly the same procedure we saw in last module. So, again, we find ourselves asking the question, in this case: so what does a covariance of 31.735 actually tell us about the relationship between X and Y?

The correlation presented in this panel attempts to answer this, by standardising the covariance with respect to the variances of X and Y. Specifically, it represents the covariance divided by the square-root of the product of the two variances (see the Appendix for a more detailed discussion of the correlation coefficient). In this case, we see that 31.735 / ( sqrt(55.98*57.75)) = 0.558. Correlations range from -1 to +1, where +1 represents a perfect positive association, -1 a perfect negative association and 0 no association. So a correlation of 0.558 implies a moderate positive association between X and Y. The square of the correlation represents the amount of total variance explained by the covariation between the two traits: in this case, 0.558*0.558 = 0.31.

As explained in the Appendix, the regression coefficients are a function of the amount of variance in one measure explained by variation in the other. As such, regression is asymmetrical, in that we can ask how well X predicts Y as well as how well Y predicts X. The standard error of the regression coefficent can be interpreted as a measure of certainty regarding that estimate. If the standard error is large, it implies that the estimated regression coefficient may not be representative of the true population value.

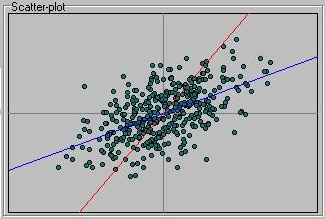
The scatter-plot represents all the points in the sample as well as the two colour-coded regression slopes.

Exploring the module

Let's use the module to get a feel for the relationship between these different measures. Firstly, note how moving either of the two specific slides, S1 or S2, changes the shape of the bivariate distribution. Increasing S1 will stretch it out horizontally (for X is represented along the horizontal axis, traditionally known as the x-axis in any case). This is because it is introducing variation in X that is not shared by Y.

Conversely, moving the S2 slider will make the distribution grow or shrink along the vertical axis. Changing the C slider has a different effect on the shape of the distribution, and its effect will be more noticeable when S1 and S2 are quite low. Set S1 and S2 to about 10 each. If C is at zero, the points should be clustered in a evenly-shaped little ball in the middle of the scatter-plot. (Make sure that the sample size is quite high, over 400 for these effects to be clear).

Note that the variance of both X and Y should be near 10. The covariance will be very small, however, and the correlation will be even smaller. The proportion of variance explained should be virtually zero. The regression slopes should also be virtually zero, so that the red line will follow vertical axis and the blue line will follow the horizontal axis. This is because, given that neither measure tells us anything about the other in this scenario, the most likely estimate of Y will be the mean of Y, for all values of X. This is represented by the blue line, the regression slope that predicts Y given X, which will be virtually flat. Likewise, the red regression slope predicting X given Y will remain very close to the mean of X at all points of Y (i.e. will tend to follow the y-axis).

If you then move the C slider to the right slowly, note what happens to all the statistics and the scatter-plot. Both variances increase, unsurprisingly, as that is what the slider is doing: adding more variation. But the covariance will increase also, as will the correlation and all the other statistics. This is perhaps best represented in the scatter-plot: a clear association between X and Y will result, in that points that tend to be higher on X also tend to be higher on Y and vice versa. The two regression lines will begin to converge, representing this fact.

With C on some high value, set both S1 and S2 to zero and observe what happens. This state of affairs implies that the only source of variation in both X and Y is completely shared. Because there is no unique variance in either X or Y, every individual's score on X would be identical to their score on Y: thus the straight line on the scatter-plot. In this case, note that the covariance equals the variance of both measures, and so the correlation is 1. Now move the C slider to a negative value: the covariance and correlation become negative, the points align themselves differently on the scatter-plot.

Try reducing the sample size to get a feel for the way in which the estimates become less consisent. With only a few points, say less than 10, you should be able to see the way in which the regression slopes can be drastically influenced by just one extreme observation. Note how the standard errors of the regression coefficients increase too - the implication of this is that the coefficients would be unlikely to be significantly different from zero, in a statistical sense.

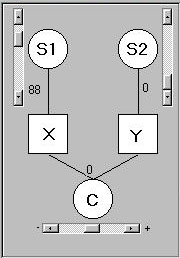Finally, we will consider a case that highlights the difference between the correlation and regression coefficients. See the following scenario, where X has a great deal of specific variation (S1=88) but there is no shared variation (C=0). As mentioned above, the program will not let a variable have zero variance (i.e S2=0 and C=0); it will add a very small amount to make the routine run. So think of Y as having a very small degree of unique variation and no association with X.

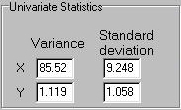We see these values reflected in the variances of the simulated sample - X has a relatively large variance, Y has a relatively small variance.

But take a look at the regression slopes, however:

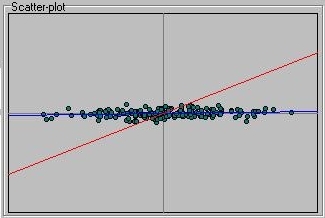
Although we know that X and Y should be unrelated, the regression slope of X on Y (that is, the red line that plots the expected value of X as a function of Y) is far from flat. If we look at the actual bivariate statistics, we see the same pattern:

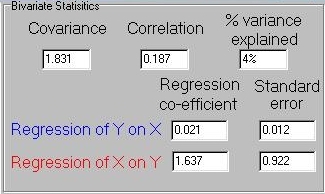
That is, despite the fact that the covariance and correlation are very small, as expected, as in the regression of Y on X, the regression of X on Y has a very large coefficient. In this particular sample there are a reasonable number of individuals, too (approximately 200), which seems to have been enough to estimate the other statistics accurately. What is going on?

The asymmetry in regression slopes is caused by the asymmetry in the variances of the two measures and is unsurprising when you think about it. It is easy to predict something that does not have very much variation - the mean will always be a good guess. Therefore, it is easy to predict Y. It is difficult for Y to predict X however, as X does have a lot of variation. Because there is such a 'restriction in range' in Y, relative to X, it is unable to accurately account for variation in X. This is reflected in the very large standard error for the regression of X on Y seen here - 0.922 (taken as relative to the magnitude of the regression slope itself, 1.637). This is why the two regression slopes tell us slightly different things: whether one variable predicts another variable better or the other way round is due to the relative balance of unique variance in each. Note that if both X and Y have the same amount of unique, 'residual' variance then both regression slopes will equal the correlation coefficient. These relations are clearly apparent in the simple equations that describe the relationship between variance, covariance, correlation and regression, as described in the Appendix.

 

Questions

  1.  

     

  2.  

     

 

 

 

 

 

 

 

 

 

Answers

     

  1.  

  2.  



Please refer to the Appendix for further discussion of this topic.




Site created by S.Purcell, last updated 6.11.2000