Maximum Likelihood Estimation (MLE)
 The likelihood ratio testModel-fitting provides a framework within which we can not just estimate the maximum likelihood estimates for parameters: we can also test whether or not they are significantly different from other fixed values. The likelihood ratio test provides the means for comparing the likelihood of the data under one hypothesis (usually called the alternate hypothesis) against the likelihood of the data under another, more restricted hypothesis (usually called the null hypothesis, for the experimenter tries to nullify this hypothesis in order to provide support for the former). For example, we may wish to ask: was the coin we tossed 100 times fair? This is rephrased as :Alternate hypothesis (HA) : p does not equal 0.50 Null hypothesis (H0) : p equals 0.50The likelihood ratio test answers this question: are the data significantly less likely to have arisen if the null hypothesis is true than if the alternate hypothesis is true? We proceed by calculating the likelihood under the alternate hypothesis, then under the null, then we calculate test the difference between these two likelihoods
2 ( LLA - LL0)
Note that if a=b/c then log(a)=log(b)-log(c). This is
why it is called a likelihood ratio test, but we look at the difference
between log-likelihoods.
The difference between the likelihoods is
multiplied by a factor of 2 for technical reasons, so that this quantity
will be distributed as the familiar
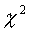 statistic. This
can then be assessed for statistical significance using standard statistic. This
can then be assessed for statistical significance using standard
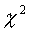 significance
levels. In most simple cases, the degrees of freedom for the test
will equal the difference in the number of parameters being estimated
under the alternate and null models. In the case of the coin, we estimate
one parameter under the alternate (p) and none under the null
(as p is fixed) so the
significance
levels. In most simple cases, the degrees of freedom for the test
will equal the difference in the number of parameters being estimated
under the alternate and null models. In the case of the coin, we estimate
one parameter under the alternate (p) and none under the null
(as p is fixed) so the
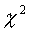 has 1 degree of freedom.
In the case of the coin tossing experiment, comparing the
log-likelihood under the alternate (i.e. when p is
estimated at its MLE) and the null (i.e. when p is
fixed at 0.50):
has 1 degree of freedom.
In the case of the coin tossing experiment, comparing the
log-likelihood under the alternate (i.e. when p is
estimated at its MLE) and the null (i.e. when p is
fixed at 0.50):
Alternate Null
----------------------------------------
p 0.56 0.50
Likelihood 0.0801 0.0389
Log Likelihood -2.524 -3.247
----------------------------------------
2(LA - L0) = 2 * ( -2.524 + 3.247) = 1.446
Therefore, as the critical significance level for a 1 degree
of freedom
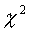 is 3.84 (see the
Probability Function Calculator also on this site) we can conclude that
the fit is not significantly worse under the null. That is, we
have no reason to reject the null hypothesis that the coin is fair. So,
the answer to the question is that the data are indeed consistent with
the coin being a fair coin.
is 3.84 (see the
Probability Function Calculator also on this site) we can conclude that
the fit is not significantly worse under the null. That is, we
have no reason to reject the null hypothesis that the coin is fair. So,
the answer to the question is that the data are indeed consistent with
the coin being a fair coin.
 Return to front page Site created by S.Purcell, last updated 21.09.2000 |