Maximum Likelihood Estimation (MLE)
MLE for twin data
How does all of this apply to twins and the kind of complex,
quantitative traits that we wish to study?
The fundamental principles of maximum likelihood still apply
in exactly the same manner as for the coin-tossing experiment. What change
are the data we measure and the form of the probability model
that describes these data.
In the case of coin tossing, we observed two items of data: n
the total number of tosses and h the number of heads. For twins,
in the most basic case, we would collect three pieces of information
for each twin pair:
- a trait measure for twin 1
- a trait measure for twin 2
- whether they are identical or not (MZ vs DZ)
For the coin tossing, we used a binomial distribution to model the data.
Typically, for quantitative traits, we would assume that our
observations come from a normally-disbtributed trait
population (bell-shaped curve). As the unit of analysis is a twin
pair (i.e. involving two variables rather than one) we need to
use the bivariate form of the normal distribution. This
specifically describes distributions of pairs of scores.
Finally, in the coin-tossing experiment we had one parameter in
our model, representing the probability of obtaining a head. In the
case of twins, we would generally have three parameters (four if we
include a means model, see below):
- a : proportion of variance
attributable to additive genetic variation
- c : proportion of variance attributable to shared environmental
variation
- e : proportion of variance attributable
to nonshared environmental variation
- m : trait mean
Traditionally, we would say the that binomial distribution takes two
parameters, n the total number of trials and p the
probability of success. A random variable, say X
that has a binomial distribution is written :
X~B(n, p)
and we are interested in P(X=x): that is, the probability
that the the random variable X has the specific value
x. In our coin tossing example, h, the observed
number of heads, is equivalent to x. Recall,
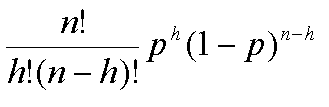 Similarly, the normal distribution has two parameters. These
parameters are in terms of the mean and variance of the distribution
rather than probabilities of success and numbers of trials.
[reword this para].These we shall call
Similarly, the normal distribution has two parameters. These
parameters are in terms of the mean and variance of the distribution
rather than probabilities of success and numbers of trials.
[reword this para].These we shall call
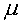 which is the trait mean and
which is the trait mean and
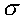 which is the trait standard deviation. A random variable,
say X that has a normal distribution is written :
which is the trait standard deviation. A random variable,
say X that has a normal distribution is written :
X~N(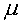 , , 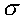 ) )
The standard formula which defines P(X=x) for
the bivariate normal distribution is
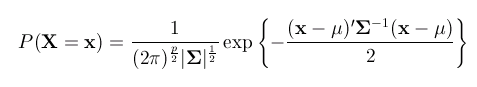 Exactly what the component terms of these formula represent is not
important - in any case, it is beyond the scope of this tutorial.
The important point to note is that the normal probability function
is determined by only two parameters (although these parameters
are actually matrices):
Exactly what the component terms of these formula represent is not
important - in any case, it is beyond the scope of this tutorial.
The important point to note is that the normal probability function
is determined by only two parameters (although these parameters
are actually matrices):
-
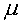 :
a vector of means (two means in the bivariate case) :
a vector of means (two means in the bivariate case)
-
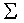 :
the covariance matrix (a two-by-two matrix in the bivariate case) :
the covariance matrix (a two-by-two matrix in the bivariate case)
(Each pair's trait scores are in the vector x and
p represents the number of variables, i.e. 2 in the
bivariate case.)
But we said that the coin tossing model only had one parameter,
and that the model we fit to twin data would have
3 or 4 parameters?
This is the distinction between parameters of a probability
distribution and model parameters. Most model fitting involves
some kind of re-parameterisation, but there is a direct
correspondence between the two types of parameters.
The following table gives the relationships:
Binomial Probability Model Coin Tossing Model
N (number of trials) ----> N (observed data)
P (probability of success) ----> P (estimated
parameter)
Normal Probability Model Twin Design Model
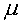 (mean vector)
----> m
(estimated or
fixed parameter) (mean vector)
----> m
(estimated or
fixed parameter)
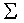 (covariance matrix)
----> a, c, e
(estimated or
fixed parameters) (covariance matrix)
----> a, c, e
(estimated or
fixed parameters)
In the case of the coin tossing experiment, there was a one-to-one
correspondence between the parameters of the binomial
probability function and the underlying model. That is, p
the probability of 'success' in the binomial model is very directly
equivalent to p the probability of getting heads in our model.
In the case of fitting a normal distribution to twin data,
parameters can either refer to the direct parameters
of the normal distribution (the mean vector and covariance matrix)
or the parameters of the underlying genetic model (proportion of
trait variation attributable to additive genetic variation, etc.)
Model-fitting for twin data proceeds by specifying the mean
vector and covariance
matrix of the normal distribution in terms of the genetic
parameters of interest. As we shall see in the next section,
this is done according to basic biometrical assumptions and allows
to us estimate quantities of interest providing we have collected
suitably informative data.
Now we are ready to model fit to twin data
As mentioned elsewhere in this course, twin analysis essentially
models the covariation between identical and non-identical twins. The
comparison of an MZ twin correlation with a DZ twin correlation allows
us to estimate the effects of additive genetic influences, shared
environmental influences and nonshared environmental influences.
Specifically, we are re-parameterising the twin covariance structure
in terms of the parameters a, c and e
(as mentioned above). The covariance matrix for a sample of twin
pairs contains three unique values:
- the variance of twin 1
- the variance of twin 2
- the covariance between twin 1 and twin 2
According biometrical theory the trait variance can be
decomposed into independent components of variance,
and the trait covariance, conditional on twin zygosity, can be expressed
in terms of these components of variance also.
- Trait variance = a + c + e
- MZ covariance = a + c
- DZ covariance = 0.5a + c
We can therefore write the trait covariance matrices for MZ and DZ
twins in terms of these three components of variance. For MZ twins
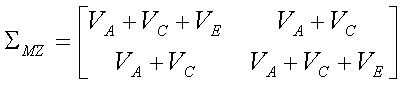 whilst for DZ twins
whilst for DZ twins
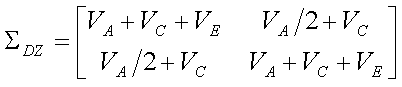 The Means Model
Because the twin design is primarily an analysis of individual
differences we are typically only interested in the components
of variance - that is, modelling the twin covariance structure. The
normal distribution requires a means model however.
We could either let
all four means (i.e. twin 1 and twin 2 for MZ and DZ twins) be
estimated independently, or we could constrain all four measures to
be estimated at the same value. The latter option would be the
typical choice: conditional on the means not being significantly
different from each other, this will provide a more
powerful test for fewer parameters are being estimated. (Note: if the
means are different in a standard twin design, this may well be
indicative of some problem in ascertainment or data management.)
Raw data versus Summary Statistics
We can either formulate models in terms of the raw
unit of observation or it may be possible to model
certain summary statistics instead. In
the coin tossing example, the summary statistics were the total number
of tosses and the number of heads. These two summary statistics
contained all of the information relevant to the problem - that is,
given these summary statistics it was not important that we knew the
actual sequence of heads and tails.
In a similar way, the mean vector and covariance matrix are said
to be sufficient summary statistics in the sense that,
under the assumption of normality, we gain nothing by analysing
the raw data (i.e. all actual scores for each twin pair) if we
know what the mean vectors and covariance matrices are for all MZ
and all DZ pairs.
Indeed, it is common practice to ignore the means model and only
analyse the covariance matrices for twins. Model-fitting to
summary statistics instead of raw data has a slightly more
complicated form, which essentially allow computational shortcuts.
These shortcuts were more or less essential in the 1960s and 1970s
when MLE techniques were first being implemented. Nowadays,
analysis of raw data is computationally not a problem.
From the point of view of using model-fitting software
such as Mx it makes little or no difference whether or
not the model is fitted to raw data or summary statistics. The main
difference is, obviously, just in how the information are entered
into the program:
The Means Model
Because the twin design is primarily an analysis of individual
differences we are typically only interested in the components
of variance - that is, modelling the twin covariance structure. The
normal distribution requires a means model however.
We could either let
all four means (i.e. twin 1 and twin 2 for MZ and DZ twins) be
estimated independently, or we could constrain all four measures to
be estimated at the same value. The latter option would be the
typical choice: conditional on the means not being significantly
different from each other, this will provide a more
powerful test for fewer parameters are being estimated. (Note: if the
means are different in a standard twin design, this may well be
indicative of some problem in ascertainment or data management.)
Raw data versus Summary Statistics
We can either formulate models in terms of the raw
unit of observation or it may be possible to model
certain summary statistics instead. In
the coin tossing example, the summary statistics were the total number
of tosses and the number of heads. These two summary statistics
contained all of the information relevant to the problem - that is,
given these summary statistics it was not important that we knew the
actual sequence of heads and tails.
In a similar way, the mean vector and covariance matrix are said
to be sufficient summary statistics in the sense that,
under the assumption of normality, we gain nothing by analysing
the raw data (i.e. all actual scores for each twin pair) if we
know what the mean vectors and covariance matrices are for all MZ
and all DZ pairs.
Indeed, it is common practice to ignore the means model and only
analyse the covariance matrices for twins. Model-fitting to
summary statistics instead of raw data has a slightly more
complicated form, which essentially allow computational shortcuts.
These shortcuts were more or less essential in the 1960s and 1970s
when MLE techniques were first being implemented. Nowadays,
analysis of raw data is computationally not a problem.
From the point of view of using model-fitting software
such as Mx it makes little or no difference whether or
not the model is fitted to raw data or summary statistics. The main
difference is, obviously, just in how the information are entered
into the program:
Raw Data
Input Output
(estimated parameters)
Twin1 Twin2 Zyg a
-0.23 -0.41 1 c
0.43 1.32 1 e
-0.47 0.76 2 m
1.23 0.65 2
-1.62 -0.44 1
... ... .
Covariance Matrices
Input Output
(estimated parameters)
MZ 1.32 a
0.87 1.28 c
e
DZ 1.29
0.54 1.35
However, analysing raw data does have certain advantages :
- outliers can be easily detected
- covariates can be easily incorporated
- missing values can be dealt with efficiently
- more complex gene-by-environment interaction models
can be implemented easily
For basic twin ACE models, fitting to covariance matrices will be
sufficient.
MLE for twin data
For the purpose of understanding MLE in the context of analysing
twin data, it is more transparent to think in terms of the
the analysis of raw data. Model-fitting proceeds in the
standard way :
- select starting values for the parameters (a, c, e, m)
- evaluate the log-likelihood for the first twin pair
using the normal probability distribution and
zygosity-specific models of the twin covariance
- sum the log-likelihoods over all twin pairs in the sample
- optimise the sample log-likelihood with respect to the
model parameters
- the output is then the values for the sample
parameters and the log-likelihood
- the likelihood ratio test can be used to compare the
full model which estimates all the parameters with
submodels that constrain one or more of the parameters
to be zero
- select the most parsimonious model that explains the data
Return to front page
Site created by S.Purcell, last updated 21.09.2000
|
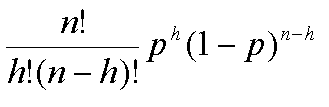
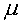 which is the trait mean and
which is the trait mean and
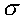 which is the trait standard deviation. A random variable,
say X that has a normal distribution is written :
which is the trait standard deviation. A random variable,
say X that has a normal distribution is written :
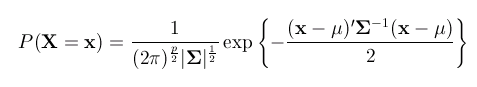
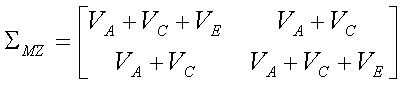
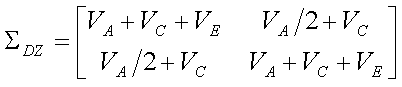
 :
the covariance matrix (a two-by-two matrix in the bivariate case)
:
the covariance matrix (a two-by-two matrix in the bivariate case)