Maximum Likelihood Estimation (MLE)

MLE analysis of linkage data

If we have a sample in which the number of recombinants and non- recombinants for two specific loci can be counted, then we can estimate the recombination fraction between between those two loci.

The test for linkage is simply the test of whether the recombination fraction (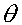

) is 0.5 (the null hypothesis of no linkage) or less than 0.5 (the alternative hypothesis of linkage).

You might have noticed a striking similarity to the coin-flipping example here. The good news is that the analysis is virtually identical. Note that, in real life, we would not expect to observe fully informative gametes for all pedigrees, and more complex methods have to fill in the gaps, but the principles are much the same.

Suppose that we observe N fully informative gametes, of which R are recombinants. How do we test for linkage and estimate the recombination fraction,

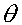Since each gamete has probability

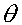of being recombinant and probability (1-

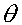) of being non-recombinant, the likelihood function is

Note : strictly speaking, the likelihood is proportional to this quantity rather than equal to it - notice that the constant part of the binomial formula has been dropped.

The log-likelihood function is therefore

The null hypothesis of no linkage implies

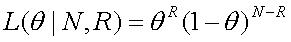
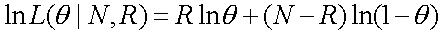
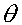=0.5, so the value of the log-likelihood function is

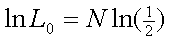
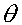As we know that the maximum likelihood estimate for

is simply the proportion of recombinant gametes

when R<(n/2), otherwise

for biological reasons Under the alternative of linkage, the maximum log-likelihood is

where R<(n/2) and

when R>(N/2).

The likelihood ratio statistic 2(lnL_A - lnL₀) provides a direct test for linkage. Note: this likelihood ratio statistics is distributed as a 50:50 mixture of chi-squared with one degree of freedom and point probability mass of 0. In this way, a one-tailed test of linkage is provided.

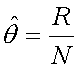
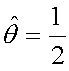
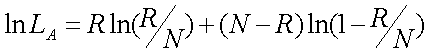
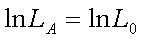
In linkage analysis, it is customary to take the common (base 10) logarithm of the likelihood function, and then define the difference between the log-likelihood at a certain value of

and the log-likelihood at

=0.5 to be the "lod-score" at that value of

. The maximum lod-score occurs at the MLE of

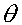: its value is equal to the likelihood ratio statistic divided by a factor of 2ln10 (approximately 4.6).

An Example

Suppose that between two loci we observe

27 recombinants
from 139 fully informative gametes

What is the evidence for linkage?

The MLE estimate of the recombination fraction is therefore

    27 / 139 = 0.1942

The log-likelihood at the MLE of the recombination fraction is

    ln L_A = 27 * ln(0.1942) + (139 - 27) * ln(1-0.1942)
       = -68.43

whereas under the null of no linkage it is

    ln L₀ = 139 * ln(0.5)
       = -96.35

This gives a value of

    2(L_A - L₀) = 2 * -68.43 - (-96.35) 
                      = 55.84

This is clearly highly significant, corresponding to a lod-score of approximately

 
   LOD = 55.84 / 4.6
       = 12.1

We can plot the lod-score curve for different values of

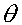From this we can draw up so-called support-intervals that give an equivalent of a confidence interval around the point maximum likelihood estimate of the recombination fraction. Typically, one would drop down one lod score unit either side of the MLE - in this case, this localises the linkage as approximately 0.13 - 0.27.

Return to front page
Site created by S.Purcell, last updated 21.09.2000