Behavioural Genetic Interactive Modules

Model-fitting to Twin Data : 2

Overview

This on-line module provides an easy way to explore the properties of the univariate ACE twin model. The user inputs the twin covariance matrices, the sample sizes and the level of significance used to compare models. The module returns the maximum-likelihood estimates for the ACE and nested submodels, determines the best-fitting model and gives standardised estimates of the model parameters for the best-fitting model.

Tutorial

Begin by entering the observed MZ and DZ covariance matrices into the forms. In the first example, all the MZ and DZ variances are 1. This is equivalent to modeling correlations rather than covariances, and will give slightly biased results in terms of model-fit. For the purpose of this module, we shall ignore this for now.

For model-fitting to work well (or work at all) the covariance matrices must conform to the basic assumptions and requirements of the model:

all four variances must be approximately equal (if not, a bad fit will result, and the module might have trouble estimating the results, and give an error-message of some kind)
the covariances must be less than the variances (this is not so much an assumption as a basic property of all properly-constructed covariance matrices: the module will crash if this is not true!)
the DZ covariance must be less than the MZ covariance: this an implication of the genetic model, and the ACE model will never fit well if this is not true (although it is possible in real life to observe this, given the nature of random sampling, etc.) Note that, even if the MZ covariance equals the DZ covariance the module sometimes gets stuck. If this happens just try repeating it a few times.

Here we see some covariance matrices that conform to these points: try entering those.

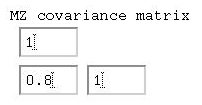
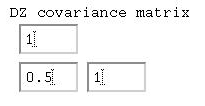Given that the 'variances' are all 1, we can say that the correlation between MZ twins is 0.80, whilst between DZ twins it is 0.50. Remembering the basic formula for calculating the heritability of a measure from the twin correlations (i.e. twice the difference) we can conclude that the trait is 2*(0.80-0.50) = 0.60, 60% percent heritability. Let's see how model-fitting compares with this estimate.

In order to begin model-fitting, we have to let the module know what sample sizes these statistics are based on. This will be important in assessing the significance of these parameters when comparing models. In this case, we have 150 MZ twin pairs and 150 DZ twin pairs.

Finally, we have to let the module know what significance level to use when deciding whether or not to reject a model in favour of a slightly worse-fitting but more parsimonious model. It is called the User-defined type I error rate in this module - it is otherwise known as the critical value, the significance level, or sometimes just alpha. This represents the probability of wrongly rejecting a model (i.e. 5% in this case).

When all of these pieces of information are entered, click the button to start the analysis. You will get an error if any of these items are missing or have invalid values (e.g. negative sample size). At the moment the module does not capture these errors, so please be careful with what you enter!

At any time the

button can be used to clear the values entered into the webpage.

The Results

The results for this particular analysis are given below: they are formatted in a way similar to how many model-fitting analyses might be reported in journals: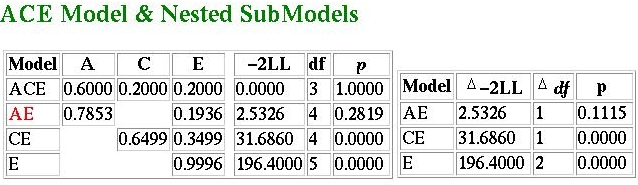

So, what do they tell us? The best-fitting model is highlighted in red - here we see that the AE model seems to provide the most parsimonious explanation of the observed data. But wasn't the heritability 60%, as we calculated by taking the difference between MZ and DZ correlations? Not under the AE model...

This represents the difference between model-fitting approaches and the more basic approach. In this case, for these particular data, the ACE model does produce best-fitting parameter estimates that concur with the correlation method. That is, the A parameter is 0.60 (representing a heritability of 60% as the total variance, A+C+E is 1). Likewise, E is estimated at 0.20 (which corresponds to 1 minus the MZ correlation in this case).

When comparing the difference in fit between the ACE and the AE model, however, the model-fitting method has determined that, given the user-specified criterion for significance, which was 0.05 in this case, the AE model does not represent a significantly worse explanation of the observed data. The model fit is in the column label -2LL. This stands for minus twice the log-likelihood, but just think of the numbers in this column as chi-squared statistics (with the degrees of freedom given in the df column to the right).

The fit for the ACE model is 0: a perfect fit. This is because the model is saturated as a consequence of the variances all being equal. The fit-function for the AE model is only 2.5326, however. This has an associated p-value of 0.2819, which suggests that, in absolute terms, the data do not depart significantly from the expected predictions of the model.

Looking at the smaller table to the right gives the model comparison tests: to ask whether the AE model provides a better fit to the data than the ACE we test the difference in fit-function against the difference in degrees of freedom. In this case, as 2.5326 - 0 = 2.5326 with 4-3 = 1 degrees of freedom is not significant at the 5% level (p=0.1115) we can conclude that the AE provides a no-worse fit to the data.

This is not the case with the CE model or the E model, however. In both cases we see that they lead to a significant reduction in fit when compared against the ACE model.

The standardised estimates for the best fitting model are given below:

Given that the total variance was 1, these simply represent rounded versions of the parameter estimates.

What if our sample had been larger, though? Say we observed ten times the number of twin pairs we had previously, but that we also observed exactly the same pattern of variances and covariances. Does model-fitting give the same results?

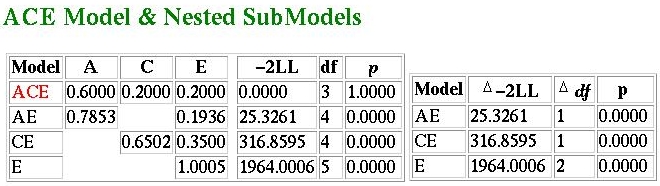In short, no! What we see here is that the ACE model is selected as the best-fitting model. The parameter values have not changed though (slight changes might occur due to the nature of optimisation). So why has the best-fitting model changed? The AE model now represents a significantly worse description of the data compared to the ACE model - this can be seen in the comparison of fit-functions. The increased sample size has directly lead to an increase in these functions (note that the chi-squared values are ten times greater - i.e. the same increase as in sample size). A chi-squared of 25.326 with one degree of freedom is significant, whereas 2.5326 is not.

Should this worry us? Were the answers 'wrong' before? No, it should not worry us unduly and it does not mean that the answers were wrong before. The difference in result represents the fact that, with the larger sample, there is essentially much more weight placed upon the exact values of the observed statistics. That is, because of the nature of random sampling, they are much less likely to be wrong (or, more to the point, the true values are likely to be much closer to the observed values than with a smaller sample). If you tossed a coin 5 times and got 3 heads, you wouldn't call it biased. If you tossed a coin 500 times and got 300 heads, you probably would (statistically speaking, you certainly should). In this case, the larger sample results in us not being able to deny the existence of a shared environmental effect amongst twins.

The standardised estimates now concur with the estimate based on twin correlations:

The reason for this is that the correlation method implicitly assumes all four variances to be equal (because they have been standardised). In the previous examples, the variances were in fact all equal (the fact they were all also equal to 1 was irrelevant here).

Of course, in real life all four variances could turn out to be equal, but usually they will not be identical. They should be similar, but not identical. Let's consider a situation such as this:

Say we observed the following MZ and DZ covariance matrices for 1000 MZ pairs and 1000 DZ pairs. Although these data are similar to the previous examples, the four variances vary themselves.

How does this impact on the model-fitting?

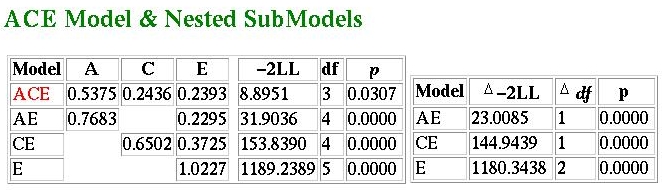
We see here that the ACE model no longer has a fit-function of zero: that is, it can no longer provide a perfect description of the data. The fit-function is 8.8951, which has a p-value of 0.0307 for three degrees of freedom. This implies that even the predictions of the ACE model significantly depart from what we have observed. As we saw in the previous tutorial, the ACE model predicts equality of variance: if this is sufficiently violated, the model will not fit. Given that, for this particular example, the sample size is quite large (1000 pairs of each zygosity) it is telling us that we have observed greater fluctuation in variance than we should expect by chance. This might indicate to the researcher to look more carefully into what is going on in the sample.

Questions

Answers

Please refer to the Appendix for further discussion of model-fitting.

Site created by S.Purcell, last updated 6.11.2000