Behavioural Genetic Interactive Modules
Single Gene Model

Overview
When we say that a trait is heritable or genetic, we are implying
that at least one gene has a measurable effect on that trait.
Although most behavioral traits appear to depend on many genes,
it is still important to review the properties of a single gene
because the more complex models are built upon these foundations.
This module aims to illustrate some facets of the basic quantitative
genetic model for single genes.
Tutorial
The Appendix introduces many of the terms that are used in
this module: it is recommended that you read it before reading
this tutorial and using the module.
Despite being called a single gene model, this module actually
allows the user to examine the effects of two genes against a
background of residual variation in a population of 1000
individuals. Let's take a quick tour to familarise ourselves
with the different elements of the module before we begin using it.
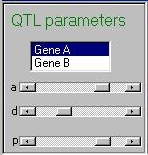 This panel allows the user to control the properties of the
two genes. Clicking on either Gene A or Gene B
will set the three sliders to the current values for that gene.
The three sliders represent the additive genetic value (a),
the dominance deviation (d) and the frequency (p) of the
trait-increasing allele. Both genes are bialleleic- that is, they
only have two alleles.
This panel allows the user to control the properties of the
two genes. Clicking on either Gene A or Gene B
will set the three sliders to the current values for that gene.
The three sliders represent the additive genetic value (a),
the dominance deviation (d) and the frequency (p) of the
trait-increasing allele. Both genes are bialleleic- that is, they
only have two alleles.
The additive genetic value can take a value between 0 and 1 in
this demo. The upper limit of 1 is arbitrary - in reality it
could be any value (it will depend on the units in which the trait
is measured). The dominance deviation, in this module,
can be between -1 and 1. Allele frequency ranges between 0 and 1.
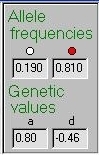 These values are represented in this panel, for the selected
gene only. In this case we see that Gene A has a common allele
(the red allele is always the trait-increasing allele), with
an additive genetic value of 0.80. In this case, heterozygotes
tend to score below the homozygote midpoint (i.e below zero)
due to dominance.
These values are represented in this panel, for the selected
gene only. In this case we see that Gene A has a common allele
(the red allele is always the trait-increasing allele), with
an additive genetic value of 0.80. In this case, heterozygotes
tend to score below the homozygote midpoint (i.e below zero)
due to dominance.
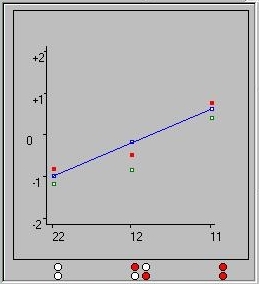 The graph plots the genetic values for Gene A. As indicated by
the key (illustrated right) the red dots here indicate the
true genetic values. The red and white circles along the
x-axis of this graph represent the three classes of genotype
for this locus.
The graph plots the genetic values for Gene A. As indicated by
the key (illustrated right) the red dots here indicate the
true genetic values. The red and white circles along the
x-axis of this graph represent the three classes of genotype
for this locus.
 The white-white genotype's genetic value is therefore plotted
at -0.80 (i.e. -a). The red-white heterozygote's value is
at -0.46 (i.e. d), whilst the red-red homozygote is at 0.80
(i.e. +a). The blue line represents the regression slope
if we assumed only additive effects at this locus. The green
points represent the mean-centred genetic values: these values
take the frequency of the genotypes into account, so that the
population mean will always be zero.
The white-white genotype's genetic value is therefore plotted
at -0.80 (i.e. -a). The red-white heterozygote's value is
at -0.46 (i.e. d), whilst the red-red homozygote is at 0.80
(i.e. +a). The blue line represents the regression slope
if we assumed only additive effects at this locus. The green
points represent the mean-centred genetic values: these values
take the frequency of the genotypes into account, so that the
population mean will always be zero.
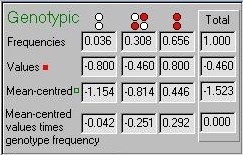 These statistics are also represented in this table, along
with the genotype frequencies. The bottom line illustrates
the way in which the population mean is always zero
based on the mean-centred genetic values.
These statistics are also represented in this table, along
with the genotype frequencies. The bottom line illustrates
the way in which the population mean is always zero
based on the mean-centred genetic values.
 We can use standard formulas to calculate the
trait variance attributable to additive or
dominance effects at each locus. These values are
in raw score units - they are not proportions of variance.
So we see that the variance attributable to the additive
effects of locus A is 0.36, and 0.02 for the effects
of dominance at this locus. As we have not set any values
for locus B yet, these values are at zero. Normally these
values would be expressed at proportions
of the overall variance - e.g. that the locus accounts
for, say, 4% of the variation in the trait.
We can use standard formulas to calculate the
trait variance attributable to additive or
dominance effects at each locus. These values are
in raw score units - they are not proportions of variance.
So we see that the variance attributable to the additive
effects of locus A is 0.36, and 0.02 for the effects
of dominance at this locus. As we have not set any values
for locus B yet, these values are at zero. Normally these
values would be expressed at proportions
of the overall variance - e.g. that the locus accounts
for, say, 4% of the variation in the trait.
The module simulates the trait scores of 1000
individuals automatically, every time one of the
sliders is moved. The variation in the individuals'
trait scores arise from two sources: variation
due to either gene A or B, and what we call
residual variation. This refers to the
net effect of all the influences that operate
on the trait other than these two genes. Potentially,
there could be thousands of such influences. The
Residual variance slider, shown in the Variance
Components panel, is used to specify the variance in
the trait due to factors other than the two genes.
We can think of the amount of residual
variation as the amount of 'noise' swamping the effects of
the specific genes.
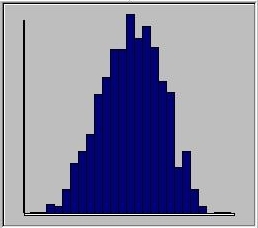 When the 1000 individuals' scores are simulated,
on the basis of the model specified, the module
plots the distribution of trait scores as a histogram.
Here we see a trait that looks more or less
normally-distributed.
When the 1000 individuals' scores are simulated,
on the basis of the model specified, the module
plots the distribution of trait scores as a histogram.
Here we see a trait that looks more or less
normally-distributed.
The slider underneath the histogram (not shown in the
screenshot) is used to adjust the scale of the x-axis,
so that the distribution can be clearly seen. The scale
ranges from +/- 1 to +/- 10.
In this instance, the module is plotting the histogram
for all 1000 individuals. By clicking on the buttons
below the histogram, however, as shown here,
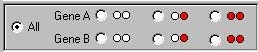 the module
will plot only those individuals with that certain
genotype. This facilitates exploration of the effect of
genes.
Using the module
the module
will plot only those individuals with that certain
genotype. This facilitates exploration of the effect of
genes.
Using the module
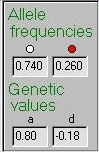 Set the module to the following scenario (make sure that locus
B has no effect on the trait: the easiest way to do this is
to close and re-open the module). This describes a single
gene with a moderately uncommon trait-increasing allele (red
allele frequency is 26%) and this red allele has a reasonably
large effect (a=0.80) with a slight effect of dominance (d=-0.18).
Set the module to the following scenario (make sure that locus
B has no effect on the trait: the easiest way to do this is
to close and re-open the module). This describes a single
gene with a moderately uncommon trait-increasing allele (red
allele frequency is 26%) and this red allele has a reasonably
large effect (a=0.80) with a slight effect of dominance (d=-0.18).
Note that, in real terms, whether or not the effect is 'large'
will depend totally on the ratio of QTL variance to residual
variance, of course.
[following section needs changing]
[make residual variance zero]
[comment on mean centering]
how pop mean always 0]
[how means of the genoptyes
equal the positions of the green dots]
[introduce concept of QTL]
Let's make the effect large by moving the
residual variance slider to the left,
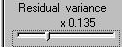 to specify that the
residual variance should only be 0.135 times the QTL variance.
If we call the QTL variance V and the total variance T, then
T = Q + (0.135*Q). The proportion of variance attributable to
the QTL (i.e. Q/T) is therefore 88%, after rearranging
the above equation. This would represent a major gene effect.
to specify that the
residual variance should only be 0.135 times the QTL variance.
If we call the QTL variance V and the total variance T, then
T = Q + (0.135*Q). The proportion of variance attributable to
the QTL (i.e. Q/T) is therefore 88%, after rearranging
the above equation. This would represent a major gene effect.
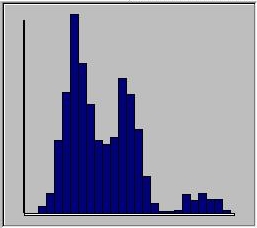 Looking at the histogram, we can see this is so. The three
genotypes separate quite clearly into three separate classes.
The height of the peaks represent the genotype frequencies.
Use the buttons to view one genotype at a time and see how
they map onto this distribution. Try changing the allele
frequencies and the genetic values to get a sense of how
they will impact on the overall distribution of the trait.
Looking at the histogram, we can see this is so. The three
genotypes separate quite clearly into three separate classes.
The height of the peaks represent the genotype frequencies.
Use the buttons to view one genotype at a time and see how
they map onto this distribution. Try changing the allele
frequencies and the genetic values to get a sense of how
they will impact on the overall distribution of the trait.
For most quantitative, complex traits we do not observe
distributions that look so discrete. There is plenty of
evidence to suggest that most genes impacting on
complex, quantitative traits will individually account
for maybe no more than 5% of trait variation. This is
equivalent to a residual variance that is 19 times greater
than the QTL variance also impacting on the trait. Set the
residual variance slider to as close to x19 as possible
and observe how little difference in the genotypic means
it is possible to observe in the histogram now.
To study the effect of two, independently acting genes,
select Gene B and change the parameter values. Note how,
if the residual variance is low, so that you can see
clearly the different genotype classes in the histogram,
you can see the pattern of genotypes of gene B if you select
on gene A in the histogram and vice versa.
Site created by S.Purcell, last updated 13.11.2000
|

 the module
will plot only those individuals with that certain
genotype. This facilitates exploration of the effect of
genes.
Using the module
the module
will plot only those individuals with that certain
genotype. This facilitates exploration of the effect of
genes.
Using the module
 to specify that the
residual variance should only be 0.135 times the QTL variance.
If we call the QTL variance V and the total variance T, then
T = Q + (0.135*Q). The proportion of variance attributable to
the QTL (i.e. Q/T) is therefore 88%, after rearranging
the above equation. This would represent a major gene effect.
to specify that the
residual variance should only be 0.135 times the QTL variance.
If we call the QTL variance V and the total variance T, then
T = Q + (0.135*Q). The proportion of variance attributable to
the QTL (i.e. Q/T) is therefore 88%, after rearranging
the above equation. This would represent a major gene effect.
 This panel allows the user to control the properties of the
two genes. Clicking on either Gene A or Gene B
will set the three sliders to the current values for that gene.
The three sliders represent the additive genetic value (a),
the dominance deviation (d) and the frequency (p) of the
trait-increasing allele. Both genes are bialleleic- that is, they
only have two alleles.
This panel allows the user to control the properties of the
two genes. Clicking on either Gene A or Gene B
will set the three sliders to the current values for that gene.
The three sliders represent the additive genetic value (a),
the dominance deviation (d) and the frequency (p) of the
trait-increasing allele. Both genes are bialleleic- that is, they
only have two alleles.  These values are represented in this panel, for the selected
gene only. In this case we see that Gene A has a common allele
(the red allele is always the trait-increasing allele), with
an additive genetic value of 0.80. In this case, heterozygotes
tend to score below the homozygote midpoint (i.e below zero)
due to dominance.
These values are represented in this panel, for the selected
gene only. In this case we see that Gene A has a common allele
(the red allele is always the trait-increasing allele), with
an additive genetic value of 0.80. In this case, heterozygotes
tend to score below the homozygote midpoint (i.e below zero)
due to dominance.
 The graph plots the genetic values for Gene A. As indicated by
the key (illustrated right) the red dots here indicate the
true genetic values. The red and white circles along the
x-axis of this graph represent the three classes of genotype
for this locus.
The graph plots the genetic values for Gene A. As indicated by
the key (illustrated right) the red dots here indicate the
true genetic values. The red and white circles along the
x-axis of this graph represent the three classes of genotype
for this locus.
 The white-white genotype's genetic value is therefore plotted
at -0.80 (i.e. -a). The red-white heterozygote's value is
at -0.46 (i.e. d), whilst the red-red homozygote is at 0.80
(i.e. +a). The blue line represents the regression slope
if we assumed only additive effects at this locus. The green
points represent the mean-centred genetic values: these values
take the frequency of the genotypes into account, so that the
population mean will always be zero.
The white-white genotype's genetic value is therefore plotted
at -0.80 (i.e. -a). The red-white heterozygote's value is
at -0.46 (i.e. d), whilst the red-red homozygote is at 0.80
(i.e. +a). The blue line represents the regression slope
if we assumed only additive effects at this locus. The green
points represent the mean-centred genetic values: these values
take the frequency of the genotypes into account, so that the
population mean will always be zero.
 These statistics are also represented in this table, along
with the genotype frequencies. The bottom line illustrates
the way in which the population mean is always zero
based on the mean-centred genetic values.
These statistics are also represented in this table, along
with the genotype frequencies. The bottom line illustrates
the way in which the population mean is always zero
based on the mean-centred genetic values.
 We can use standard formulas to calculate the
trait variance attributable to additive or
dominance effects at each locus. These values are
in raw score units - they are not proportions of variance.
So we see that the variance attributable to the additive
effects of locus A is 0.36, and 0.02 for the effects
of dominance at this locus. As we have not set any values
for locus B yet, these values are at zero. Normally these
values would be expressed at proportions
of the overall variance - e.g. that the locus accounts
for, say, 4% of the variation in the trait.
We can use standard formulas to calculate the
trait variance attributable to additive or
dominance effects at each locus. These values are
in raw score units - they are not proportions of variance.
So we see that the variance attributable to the additive
effects of locus A is 0.36, and 0.02 for the effects
of dominance at this locus. As we have not set any values
for locus B yet, these values are at zero. Normally these
values would be expressed at proportions
of the overall variance - e.g. that the locus accounts
for, say, 4% of the variation in the trait.
 When the 1000 individuals' scores are simulated,
on the basis of the model specified, the module
plots the distribution of trait scores as a histogram.
Here we see a trait that looks more or less
normally-distributed.
When the 1000 individuals' scores are simulated,
on the basis of the model specified, the module
plots the distribution of trait scores as a histogram.
Here we see a trait that looks more or less
normally-distributed.
 Set the module to the following scenario (make sure that locus
B has no effect on the trait: the easiest way to do this is
to close and re-open the module). This describes a single
gene with a moderately uncommon trait-increasing allele (red
allele frequency is 26%) and this red allele has a reasonably
large effect (a=0.80) with a slight effect of dominance (d=-0.18).
Set the module to the following scenario (make sure that locus
B has no effect on the trait: the easiest way to do this is
to close and re-open the module). This describes a single
gene with a moderately uncommon trait-increasing allele (red
allele frequency is 26%) and this red allele has a reasonably
large effect (a=0.80) with a slight effect of dominance (d=-0.18).
 Looking at the histogram, we can see this is so. The three
genotypes separate quite clearly into three separate classes.
The height of the peaks represent the genotype frequencies.
Use the buttons to view one genotype at a time and see how
they map onto this distribution. Try changing the allele
frequencies and the genetic values to get a sense of how
they will impact on the overall distribution of the trait.
Looking at the histogram, we can see this is so. The three
genotypes separate quite clearly into three separate classes.
The height of the peaks represent the genotype frequencies.
Use the buttons to view one genotype at a time and see how
they map onto this distribution. Try changing the allele
frequencies and the genetic values to get a sense of how
they will impact on the overall distribution of the trait.