Univariate Twin Analysis

S.Purcell, 2000.

Introduction

In this tutorial we shall take a look at a dataset containing scores for 500 MZ twins and 500 DZ twins on a single measure. The aim of these particular analyses is to determine whether or not there is any evidence for a genetic effect on the trait.

The dataset can be downloaded here. Depending on your browser, you might have to right-click and choose 'Save As...' or 'Save Target As...'. Alternatively, you might be able to left-click on the link to view the raw data in your browser window and then copy-and-paste the dataset into WordPad or some other text-editor and save it from there onto your computer.

The dataset is in comma-separated value format so it can be read by almost any program, including Excel. Each row of the dataset represents information on one twin pair. It contains four variables:
  • An ID number for each twin (we can ignore these)
  • The zygosity of the twin pair (1 for MZ, 2 for DZ)
  • The trait score for the one twin (t0_1)
  • the trait score for the other twin (t0_2)
If you have access to Stata, open it up, after you have transfered the datafile to your computer. If you do not have access to Stata, open up whichever statistics package you are most familiar with. A spreadsheet such as Excel could even be used for most of these analyses.

In the Stata command line, type the following to load the raw data into memory, replacing the u:\ path with the appropriate path for your computer. The comma option after the filename tells Stata to expect a comma-separated value file.

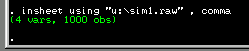Assuming it loads correctly, you should see the following text in the output window. This simply confirms the fact that our data file contains 4 columns (i.e. the variables as listed above) and 1000 observations (i.e. 500 MZ twin pairs and 500 DZ twin pairs).

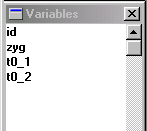The Variables window in Stata should display the names of the four variables. These were the top row of the raw datafile (often called the header row). Unlike SPSS, Stata does not provide a spreadsheet-style view of the data by default. Although it can sometimes be useful to literally see all your data on the screen, when working with large datasets, as is typical in quantitative genetic research, the spreadsheet-style view becomes less useful.

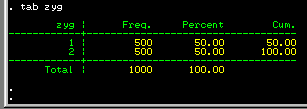The tab command in Stata is used to tabulate values of a variable to produce a frequency table. Type in tab zyg to get a breakdown of the zygosity status of the sample. If all is well, this should confirm that you have successfully loaded 500 pairs of each twin zygosity into Stata.

The trait scores for each twin (t0_1 and t0_2) are continuously-distributed variables, so it is not informative to tabulate each the values in the same manner as above. Rather, we have to rely on summary descriptive statistics such as the mean and variance to tell us about the distribution. The command su (summarise) can be used to give these statistics. If you type su t0_1 t0_2 Stata will print the mean for all twin 1s and all twin 2s separately, as well as several other useful statistics such as the standard deviation.

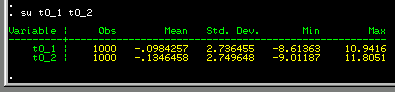We can see that there is no real difference between the mean scores for all twin 1s and all twin 2s. Also, there is no real difference in the variability of these variables: the standard deviations are very similar.

Another useful way to look at data is to plot it. To generate a histogram for all twin 1 scores, type the following:

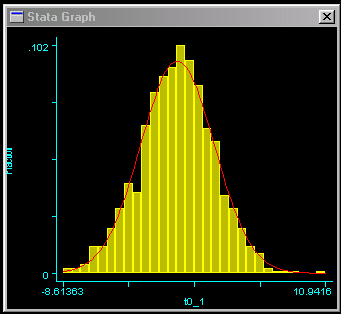The bin(30) option tells Stata how many bars (or bins) to draw in the histogram and the norm option is used to plot a normal curve over the histogram, drawn in red.

This should result in the graph as shown to the right. We can see that the trait is approximately normally distributed, which is good news for these analyses.

 

 

 

 

 

 

 

In genetic analyses, we are often more concerned with the relationships in scores between related individuals. An ideal way to get a sense of the relationship between two continuously-distributed measures is to draw a scatter-plot of the two variables. We can use the following command to plot the scores of one twin against the scores of the other twin.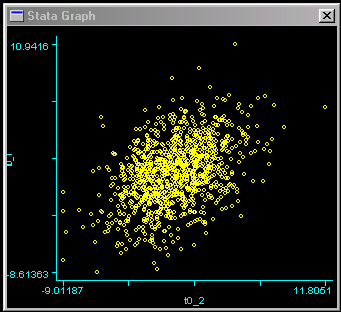

Instead of producing a histogram, Stata realises that we have specified two variables after the graph command and so produces a bivariate scatter-plot.

Each dot represents a twin pair: the position on the vertical, or y, axis represents the score for the first twin, the position on the horizontal, or x, axis represents the score for the other twin. We can see evidence of an association between twins here: the distribution is slightly more drawn-out going from bottom-left to top-right. That is, individuals who score low are more likely to have co-twin who also scores below average, and vice-versa. The association is by no means strong, however.

 

 

 

We can quantify this association between scores with a correlation coefficient. Type the command as shown to the right for Stata to calculate the correlation between twins for this trait.

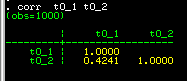Stata displays the following correlation matrix: the correlation is 0.4241. This will undoubtably be significantly greater than zero (the command pwcorr t0_1 t0_2, o sig can be used to also give p-values for the correlations).

So far, all the graphs and statistics have not differentiated between MZ and DZ twins. The aim of this analysis is to compare twin similarity between MZ and DZ twins, so we need to analyse twins separately by their zygosity.

Type the command sort zyg to sort the dataset by this variable. It is now possible to stratify analysis by twin zygosity. That is, rather than giving the twin correlation for all twins, Stata will output the twin correlation for MZ twins and DZ twins separately.

Looking first at whether there are any differences in means or standard deviations between MZ and DZ twins, use the command as shown to the right.

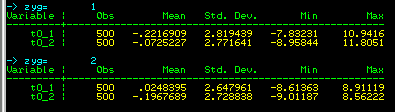The output of this command, shown left, is now broken down for MZ and DZ twins: we can see that there is no big difference between MZ and DZ twins in terms of their trait means or standard deviations. (Formally, we would test these statistically, but an 'eye-ball test' will suffice for present purposes.)

Now enter the following command, shown to the right, in order to obtain the twin correlations for MZ and DZ twins separately: these quantities are fundamental to the twin analysis we are about to perform.

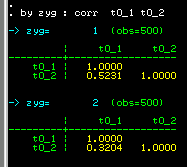We see that the MZ correlation (0.5231) is larger than the DZ correlation (0.3204). So the correlation we obtained earlier for the whole sample, ignoring twin zygosity, effectively represented an average between these two figures.

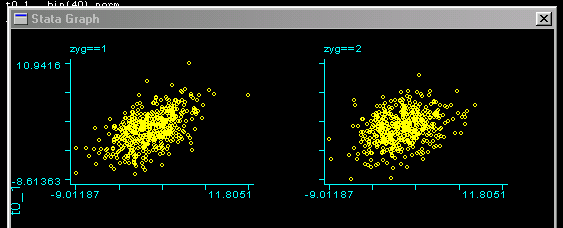
Looking at the scatter-plots by zygosity we can see this difference in correlations: the left scatter-plot is for MZ twins, the right one for DZ twins. We can see a slightly stronger relationship for MZ twins.

As mentioned in the Appendix text, a significantly larger MZ correlation compared to DZ correlation is evidence for the existence of genetic influence on a trait. The standard method of estimating heritability from twin correlations is as follows (also described in the Appendix):
  • Heritability is twice the difference between MZ and DZ correlations
  • Proportion of variance due to environmental factors shared between twins equals the MZ correlation minus the heritability
  • Proportion of variance due to environmental factors not shared between twins equals 1 minus the MZ correlation
We can use the di (for display) command in Stata to act as a pocket calculator: the estimate for heritability is therefore approximately 40% (i.e. twice the difference between MZ and DZ correlations is 0.4054). The shared environment accounts for 12% of variation, whilst nonshared environmental effects account for just under half of the variance in this population. The last line merely confirms that these proportions of variance do in fact add up to 1, as they should

Covariances and Model-fitting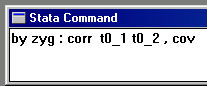

These estimates of heritability are based on the comparison between correlations. As mentioned in the Appendix, it is often preferable to analyse variances and covariances instead, for a number of reasons. We can obtain the variance-covariance matrices for MZ and DZ twins from Stata by adding the cov option to the correlation command as shown to the right.

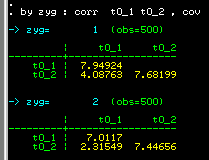As we saw earlier, there are no major differences between four estimates of variance. We can apply model-fitting methods to these variance-covariance matrices and compare the results to the simple analysis with correlations.

 

 

 

We can use the Model-fitting 2 module from the main BGIM site. Clicking on the WWW symbol shown below enters the module designed to perform model-fitting analysis on univariate twin data.

Model-fitting 2
This on-line resource performs a maximum-likelihood analysis of univariate twin data and presents the parameter estimates for nested sub-models. The tutorial explains how to use the module and how to interpret the output.

 

We can simply enter the MZ and DZ variances and covariances estimated by Stata into this module: the picture to the right shows these. Also, we must specify how many MZ and DZ twins these variances and covariances were based on - 500 each in this case. Not shown here, the module also asks for a Type I error rate : just enter 0.05 for this. This represents the chance of falsely rejecting a model, as described in the Appendix and other modules.

 

 

 

 

 

 

The results of this analysis are shown below: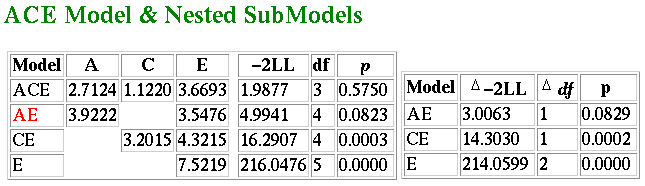

The figures represent components of variance. From the full ACE model we obtain a similar estimate of heritability as from the correlational analysis. The total variance is 2.7124 + 1.122 + 3.6693 = 7.4937. Therefore the proportion of variance due to additive genetic effects, or heritability, is 2.7124/7.4937 = 0.36. In other words, the model-fitting analysis estimates that 36% of the variation in the population is due to genetic effects. This can be regarded as a more accurate estimate than the 40% obtained from analysing correlations. The reason for the difference is that the model-fitting analysis is taking into account the small differences amongst the four variances.

We also see that the best-fitting model is in fact the AE model: that is, the effect of shared environment is not significant. A model with only additive genetic and nonshared environmental effects is shown on the second line (again, go to the module tutorial for a full explanation of all the figures in this table). The standard estimates from the AE model are given below: the impact of genes is estimated much higher now:

 

 

Further exploration: Simulation

The datafile we used in the analysis above was not collected from real individuals measuring any particular trait: it was simulated, using the SIMULATOR module at this website.

SIMULATOR
This on-line resource allows users to easily simulate multivariate ACE datasets and explore the properties of the Cholesky decomposition description of data.

When using simulated data, we have the advantage of actually knowing what the answers should be because we have simulated the dataset according to these values. In the univariate case, this module allows you to create a random dataset of a specified number of MZ and DZ twin pairs whose scores are as if they come from a population for which the various quantities we estimated above are known.

In the simulation module, the relative balance of additive genetic, shared environmental and nonshared environmental effects are specified in terms of the path-coefficients rather than as variance components or proportions of variance. See the Appendix for the distinction between path co-efficients and variance components: essentially we simply square the path co-efficient to give the variance component (think of path tracing rules- we traverse the path twice for the trait variance). The following path co-efficients were used in the simulation of the dataset:

By selecting the Calculate option, the module gives the corresponding proportions of variance attributable to A, C and E. In this case the total variance is there therefore 9 (2*2 + 1*1 + 2*2). The proportion of variance due to additive effects of genes is (2*2) / 9 = 44.4%. In a similar manner, we calculate that the shared environment accounts for 11.1% of variance, the nonshared environment for 44.4%.

In infinitely large samples, the methods of analysis used here would have yielded these exact figures. Instead, because of sampling error, the estimates were slightly off, even though the sample sizes seemed reasonably large.

Try using the simulation module to create another dataset according to the same properties, analyse it, and you will notice that the estimates will be slightly different again. But if you repeated this a large number of times, you should also notice that the estimates may be a little out each time, but there should be no consistent bias in them (i.e. such as the heritability being consistently over-estimated).

Bear in mind, however, the simulation module simulates data according to very simplistic assumptions that might not hold in real life, which potentially could lead to systematic bias. An example of this would be the equal environment assumption, as mentioned in the Appendix.

Try simulating a univariate dataset with different values, and then use Stata to calculate the correlations and covariances. Try experimenting with the approximate size of samples you need before the estimate become stable.

Further exploration: Using Mx to perform the analysis

Try installing Mx on your computer and run the basic ACE script to perform the same analyses. The basic ACE script can be found here. You will need to edit the script just to enter the covariance matrices, as follows: 
Group2: MZ twin pairs
Data NInput_vars=2 NObservations=500
     CMatrix 
	7.949
	4.088 7.682
and for DZ twins 
Group3: DZ twin pairs
Data NInput_vars=2 NObservations=500
     CMatrix 
	 7.012
	 2.315 7.447
Looking at the output, you will see the relevant parameters A, C and E representing the components of variance. These will correspond very closely to the values obtained from the model-fitting module above. In this case, 
 
  MATRIX A
 This is a computed FULL matrix of order    1 by    1
  [=X*X']
             1
 1      2.7139
  
  MATRIX C
 This is a computed FULL matrix of order    1 by    1
  [=Y*Y']
             1
 1      1.1213
  
  MATRIX E
 This is a computed FULL matrix of order    1 by    1
  [=Z*Z']
             1
 1      3.6684
The script also contains a standardisation group, so the proportions of variance are also given (T, U and V correspond to A, C and E respectively). 
  MATRIX T
 This is a computed FULL matrix of order    1 by    1
  [=D~*A*D~]
          1
 1   0.3617
  
  MATRIX U
 This is a computed FULL matrix of order    1 by    1
  [=D~*C*D~]
          1
 1   0.1494
  
  MATRIX V
 This is a computed FULL matrix of order    1 by    1
  [=D~*E*D~]
          1
 1   0.4889
This gives the same heritability estimate, 36%. The fit statistics are also important: 
 Your model has    3 estimated parameters and      6 Observed statistics
  
 Chi-squared fit of model >>>>>>>     1.984
 Degrees of freedom >>>>>>>>>>>>>         3
 Probability >>>>>>>>>>>>>>>>>>>>     0.576
The non-significant fit (p=0.576) represents that the model accounts for the observed data well.

The script can be modified to test an AE model- remove the free keyword after the Y matrix from the first group: 
	Begin Matrices;
		X Lower nvar nvar free    ! genetic structure
		Y Lower nvar nvar         ! shared environment 
		Z Lower nvar nvar free    ! non-shared path co-efficients
	
		H Full 1 1
	End Matrices;
As can be seen this gives similar results to the model-fitting module above: 
  MATRIX T
 This is a computed FULL matrix of order    1 by    1
  [=D~*A*D~]
          1
 1   0.5252
  
  MATRIX U
 This is a computed FULL matrix of order    1 by    1
  [=D~*C*D~]
          1
 1   0.0000
  
  MATRIX V
 This is a computed FULL matrix of order    1 by    1
  [=D~*E*D~]
          1
 1   0.4748
Try using Mx to test the CE model; try analysing other univariate twin covariance matrices.

The next tutorial will consider the multivariate extension to these analyses.



Site created by S.Purcell, last updated 30.11.2000